拘束を与えると言うことは行列解法でどういう事をしているのか?(R-2)
FEMにしろ、Spiceにしろ、どこか1点以上、基準となる変位拘束(電位拘束)を与えなければ行列式は解けない。
と言うことは、行列解法時に拘束条件はどのような扱いになっているのかは確認しておく必要がある。
簡単に3×3の行列を取り上げる。
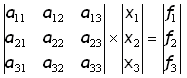 をFEMで言う全体剛性マトリックスと変位、力の関係と捉え、 をFEMで言う全体剛性マトリックスと変位、力の関係と捉え、
変位拘束X1=0を与える事を考える。
もともと、行列表記は多数の方程式の簡易表記なのであるから元の方程式群に戻してみる。
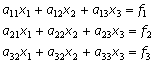 でX1=0なのであるから でX1=0なのであるから 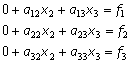
であり、このままでは変数が2個で、式が3個という変則な解けないマトリックスになる。
しかし、変位拘束"0"を与えたということは次のように、f1について解けない(解く必要がない)事を意味している事を忘れてはならない。
(Y=AX+BでX,Yを同時に規定できない様に、同じ点の変位と力は同時に規定できない)
従って、行列は次の様に縮退できる。
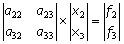
ここで縮退に伴って捨てられたa12・X2+a13・X3=f1 は決して0ということではなく、有限の値を持つ事を忘れてはならない。
つまり、
変位拘束を与えるということは、その見返りに、力については他の計算結果を無条件で受け入れる
事なのである。これが、拘束の応力を規定できない(=特異点)一因になっている事を忘れてはいけない。
もう少し説明すると、
・X方向変位を固定したという事は、「X方向の力を無条件に受け入れる」。ということであり、
・X方向拘束点では、力はX方向へ流れており、
・Y方向 〃 Y方向へ流れている。
従って、XY拘束をした点ではその拘束点に向かって放射状に力が流れこんでいる。
片持ち梁で、固定端を完全固定すると、最大曲げ応力発生点と応力吸収点が同居することになり、応力が計算出来ない特異点になるのである。
他の現象に例えて言うなら
- 発熱点を温度一定に保つようなもの。どれだけ発熱しようが、温度が上がず、安定発熱量は有りません。
- 電源を短絡するようなもの。どれだけ電流が流れようが、電圧は上がらず、安定電流は有りません。
|